|
Phobos, Moon of Mars |
||||
|
.. July 22, 2009 Former astronaut Buzz Aldrin spoke about the future of space exploration and said the public would be interested in a monolith on Phobos, one of the two small moons that revolve around Mars. |
||||
Related Links:
|
||||
| The Monolith on Phobos
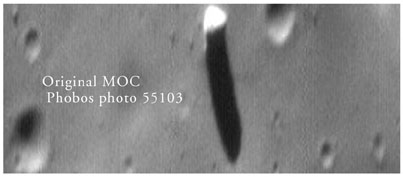
In 1998, the Mars Global Surveyor took several photographs of Marsí satellite Phobos with its high-resolution camera. On seeing this image some time ago, I noticed what appeared to be an unusual formation in the processed version of image SP255103 that I downloaded from the MGS Archive maintained by the United States Geological Survey (USGS). My interpretation, however, was that while it was interesting, it could probably be explained as a rounded boulder casting a long shadow due to a low sun elevation. Mr. Efrain Palermo had also examined this image and came to a conclusion considerably different than my own. He had noticed something of possible significance that I had missed on my cursory examination: the white streak extending down from the left side of the object (or out from its base along the ground, in my interpretation). To him, this suggested that what I saw as a "dome-like rock" embedded in the surface of the moon was in fact only the "roof" of a vertical tower. The adjoining white streak, in his interpretation, was a small part of the vertical side of this tower illuminated by sunlight, the rest of it being hidden in the object's own shadow. We discussed the image via email. I objected that the problem with his interpretation was that the orientation of the long axes of the crater ellipses in the image suggested strongly that the MGS took the image from almost a horizontal position relative to the moon's surface. It seemed to me that the camera was to the left relative to the image and looking towards the right across the moon's surface, with the horizon somewhere past the image's right edge. Any tall structure should be oriented in the direction of the short axes of the crater ellipses in an image taken from a near-horizontal perspective. In this case, it seemed that a tower should extend from the left of the image to the right, not from the bottom toward the top as Efrain proposed. The image as Efrain and I first saw it is shown in Figure 1.
To make sure that the spacecraft viewing angle was as low as it appears in the image, I referred to the image data on the USGS archive of MGS images. The data for SP255103 is at: ftp://ida.wr.usgs.gov/cdroms/MGSC_0010/index/imgindx.tab I was surprised to find that the viewing angle was not low at all. The "emission angle," which is in the thirteenth column of each image listing, was 19.84 degrees. The emission angle is the angle off the vertical direction of the planet surface to the camera, so the spacecraft was looking almost straight down from above, at an elevation angle of 90 minus 19.84 degrees or 70.16 degrees. But why are the craters so elongated? It is because the image we both were looking at was a processed JPEG version we had downloaded from the browser page for the image at: http://ida.wr.usgs.gov/html/orb_0551/55103.html. The craters are deceptively elongated in the processed image because it was stretched for some reason. The raw image shows nearly circular craters, as would be expected for the low emission angle. Efrain's interpretation of the object is shown on the version of the image below that I had corrected by stretching the image until the craters were circular rather than elliptical. His interpretation of the object is shown in Figure 2.
The raw image is also available on the browser page, and it turns out my "orthorectification" was unnecessary. The section from the raw image is shown in Figure 3. The contrast has been adjusted but the image dimensions have not been altered from the raw image in any way. It is virtually identical to my orthorectified version. This should be very close to how the object actually appeared to the camera.
There seems to be no good reason to put the word "monolith" in quotes to describe this object. Efrain's interpretation is absolutely correct. At the very least, this object is a monolithic block of stone, although it's high reflectivity may indicate that it is composed of something else. But how likely is it that it's artificial? That depends in part on how tall the object is relative to the width of its base. A block of stone several times longer than its height created from the impact of some large meteoroid would be unlikely to land on its narrow end and remain upright. The greater the height-to-width ratio, the less likely it is that this monolith was placed on the surface of Phobos by the forces of Nature. On this question, the MGS image data has another surprise: the incidence angle (in the fourteenth column of each image listing) for the principal (center) point in the photograph is 43.47 degrees. The incidence angle is the angle between the sun and the vertical direction relative to the surface being imaged. The height of an object can be simply computed as the length of its shadow divided by the tangent of the incidence angle. The length of the shadow is 53 pixels and the width of the object is 15. The tangent of the 43.47 degree incidence angle is 0.948, implying a height-to-width ratio of 53 / (15 * .948). This would make the height of the object 3.7 times its width. These are the proportions of a skyscraper, not of a natural object. And with the stated image resolution of 2.4 meters per pixels, the object would be the height of a forty-two-story office building! But before getting carried away with the notion of an immense building rearing up from the surface of Mars' moon Phobos, a little cautious consideration of what the image data really means is in order. Determinations of an object's height from shadow length and sun angle depend upon knowing the sun's elevation above the surface on which the shadow is cast. Unfortunately, the sun elevation for spacecraft images only tells us the sun's elevation at a point on a perfect sphere centered on the targeted planet or moon. And Phobos is far from a perfect sphere. Its dimensions are 27 X 21.6X 18.8 kilometers. It is 40% wider at its greatest width than it is at its most narrow width. Even for a world that is spherical in shape, there can be considerable variations in local topography - hills and valleys - that make the implications of shadow length uncertain. This was a problem with the "Blair Cuspid" objects on the Earth's moon. However, there are ways to estimate the true sun angle on a sloping surface from image brightness variations. These methods are based on the knowledge that the moon is, on average, a nearly perfect sphere. These methods, as applied to the Blair Cuspids are described at: http://www.vgl.org/webfiles/lan/cuspids/cuspids.htm (NOTE: Further review of MGS image data indicates that the non-spherical shape of Phobos was in fact accounted for in the computation of the stated sun elevation. See 2/15/00 update). But there is another clue besides the shadow length that suggests this monolith on Phobos has an appreciable height: the craters are nearly circular, indicating the spacecraft was looking almost straight down at the surface at this point in the photograph. Yet the vertical edge of the object (outlined in red in Figure 2) is still 14 pixels long. If the object is upright relative to the surrounding surface, it would still be twice the height of the apparent width of its base assuming that the emission (viewing) angle of the camera was the stated 19.84 degrees at this point in the photograph. Although assumptions about the actual camera viewing angle are uncertain for essentially the same reasons that assumptions about the sun angle and shadow length are, it does provide an estimate of height independent of the estimate based on the shadow length. Both ways of estimating indicate an extremely unusual object may stand on the surface of Phobos. Figure 4 shows Efrain's idea of what this object might look like viewed from the surface. While I think it may be more vertical and with a sloping "roof," rather than leaning to one side as he does, his mock-up seems a reasonable and perhaps even a conservative depiction. The dimensions he gives the object make its height twice the width of its base (only about 28 stories high rather than 42 as implied by the shadow length). It could well be much higher...
Despite the uncertainties in these estimates of the object's shape, it clearly is unusual enough to warrant another look. A single image taken from the nearly horizontal perspective in Figure 4 would be most informative. Unfortunately, the Mars Global Surveyor, now in a low mapping orbit around Mars, will never have another close encounter with Phobos. That will have to remain the task of some future spacecraft. Given NASA's history of avoiding any intentional examination of anomalous objects, it will probably have to happen by accident. But Phobos is a very small world, so if other spacecraft have close encounters with Phobos in the future, there is a fair chance we eventually will see this monolith again. --- Lan Fleming Efrain would be interested in any comments or questions
on his discovery. He can be contacted at:
See second image and some of the other unusual objects from the first image in the 2/15/00 update. VGL
|
||||
Phobos Update: 2/15/2000
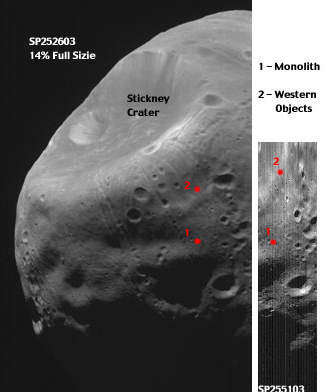
SP255103 was not the only image of Phobos taken by the MGS. There were five other high-resolution images acquired. And one of them, SP252603, also shows the "monolith," but at 5.3 time lower resolution. While the lower-resolution image provides less detail of the object, it provides something equally useful: context. Figure 1 shows the two images for comparison. It can be seen from the longer shadows in craters that the sun angle of SPS252603 is noticeably lower than in SP255103. But yet the Monolith, (labeled 1 on both images) is still a large distance away from the day/night terminator. This is important because the shadows of small objects become progressively longer as the sun sets and the terminator approaches, until eventually common boulders can cast long shadows that look like they are being cast by enormous towers This second image indicates that is not the case for the monolith.
An enlargement of the section of SPS252603 containing the monolith is shown together with the section of SP255103. The former has been enlarged by a factor of 2 while the latter has been reduced in size so that they are roughly comparable. The shadow cast by the monolith in SPS252603 is noticeably longer - about 50% - than it is in SP255103, consistent with the lower sun angle in SPS252603.
in SPS25103 reduced in size for comparison of shadow lengths. 2. Other Interesting Objects in SP255103 As noted by several people, there are other objects in this image casting interesting shadows. Some of them are so close to the terminator that it seems probable that they are just boulders or rock fragments with elongated shadows. However, there is a group of objects with elongated shadows at a position much farther from the terminator than the monolith, as can be seen in Figure 1 where their position is marked by a dot labeled "2". Their sunlit position makes at least the tallest of them even less likely to be just boulders or rock outcroppings of the sort that would be expected on an airless moon. Several objects of this group are shown in Figure 3 below, including the tallest.
Notice that there is no shadow in the adjacent crater, another indication of a high sun angle. It seems quite possible that these objects are actually much taller than the lengths of their shadows might suggest, given the apparently high sun elevation. These objects are much smaller than the monolith, so the above image has been enlarged. It was also "orthorectified" by stretching the image until the nearby craters were round. The craters in the western (upper) part of the raw image are extremely elliptical in shape. That could be explained by a difference in resolution in the vertical and horizontal directions of the image plane that is in turn related to the scanning rate of the camera as the spacecraft rotated to sweep the 1-pixel wide array of CCD elements across the moon. Alternatively, it might be explained by an extreme off-nadir viewing angle of the region in that part of the image. The latter cause is familiar to anyone who has seen a few spacecraft images of planets or moons. As shown in Figure 4, the MSSS processed version that most people would see when browsing the USGS archive, further distortions were introduced by the stretching of the already distorted raw image, making these features virtually unnoticeable. There are other "orthorectified" images in the MGS archive that were stretched to make the craters look round. In this case, however, the rectification worked only for a few craters at the bottom of the image near the shadow terminator. The stretching operation distorted the rest of the image, particularly toward the top.
Right: JPL/MSSS enhancement. Both are full scale. The complete processed image is available at: http://ida.wr.usgs.gov/fullres/complete/orb_0551/55103.jpg 3. More Information On Interpreting the Sun Elevation Each set of images in the USGS archive is accompanied by an "errata" file that describes known errors in the image data listings. To see if the extraordinarily high sun elevations cited for the Phobos images containing the monolith might be in error, I looked at the errata file for the set that included all the Phobos images. This text file is at: ftp://ida.wr.usgs.gov/cdroms/MGSC_0010/errata.txt Rather than finding any error correction, I found a statement that reinforces the likelihood that the monolith and other objects have long shadows because they are extraordinarily tall objects: All images from the Phobos orbits (476, 501, 526, and 551) were processed with Phobos position information from the NAIF SP kernel file mar033-5.bsp. Owing to limitations in our processing software, coordinate information is relative to the IAU triaxial ellipsoid model of Phobos in some instances, and relative to a spheroid with equatorial radius 13.4 km and polar radius 9.2 km in other instances, and should be treated with some caution. C-kernel information was not available for Phobos images 526/01, 526/02, and 526/03, and in these cases the ancillary values are grossly in error. The "C-kernel" software computes positions of the spacecraft relative to the target and does not appear to have any bearing on the sun elevation data. The primary reservation I expressed in the previous article about taking the surprisingly high sun elevation too literally was the irregular shape of the moon. But if either the "triaxial ellipsoid" model or the spheroid model was used to compute the sun elevation, there seems to be little reason to believe it was more than a few degrees different from the stated angle. Either of these models should be more accurate than the simple spherical model that I had conjectured might explain an overly high sun elevation - and an overly great height-to-width ratio of these objects. Caution, of course, is still needed as this file says. It may be that the shadows of these objects are very long because they are being cast down slope. There is no obvious indication of this in the images, however. A slope of approximately 30 degrees from the horizontal would be needed for an object whose height-to-width ratio was only 1:1 to cast a shadow as elongated as that of the monolith for a sun elevation of 45 degrees. It seems such a steep slope would be more noticeable. 4. Estimate of Sun Elevation at Position of Monolith There is a quantitative estimate that can support this seeming lack of a steep slope. As noted previously, the sun elevation stated in the image data listing applies only to the central point in the image and only for a surface that is in the horizontal plane of the model of the moon being used. The sun may be much higher or lower at points other than the center of the image. But given the sun elevation at the central point, there are methods to determine the slope angles at other points. In The Martian Enigmas, Mark Carlotto describes the basis for a shape-from-shading technique based on a simple relationship between brightness and slope that is applicable under the following conditions:
This relationship between digital image brightness, B, and the sun incidence angle, A, relative to the surface normal (perpendicular relative to the surface) of a slope is: B = K cos(A) + D, where K is some constant, D is the digital brightness for the points in the image where there was a complete absence of light. For the first image, the blackness of space around Phobos can be used for D and in the second, there is total shadow toward the bottom. The value of K for an image can be computed from the measure brightness at the center, Bc and the stated sun incidence angle, Ac. K = (Bc - D) / cos( Ac ) To compute the value of the constant K, I measured the average brightness for a square consisting of a hundred pixels near the center of both images. After determining K, I measured the brightness for a small strip of pixels running along the length of the Monolith's shadow and then computed the estimate of the sun incidence angle at the position of the Monolith as: Ax = acos( (Bx - D) / K) The sun's elevation, Ex, is 90 degrees minus the incidence angle, Ax. After running through the measurements several times, selecting slightly different sets of pixels for both the center points and the monolith's position, the best estimate seemed to be a sun elevation at the position of the monolith of 28.1 degrees for the first image and 38.5 degrees for the second. The height, H, of an object can be computed from the length, L, of the shadow it casts at a sun elevation angle, E, simply as: H = L tan(E). Assuming the sun elevations I estimated for the two images are accurate, the ratio of the lengths of the shadows cast by the Monolith in the images should be: These sun elevation estimates imply a height-to-width ratio for the Monolith of 2.5 to 1. That would mean the Monolith is "only" 28 stories high rather than the possible 40 stories that would be the case if the stated sun elevation at the center point in the image was applied directly to the Monolith's position. This still makes Efrain Palermo's mock-up, with a height-to-width ratio of about 2 to 1, a conservative speculation about the true proportions of the Monolith. This new information gives sound reason, in my opinion, to believe that these objects deserve serious investigation by NASA, even if they ultimately prove to be less unusual than they now appear to be. -- Lan Fleming VGL
|
||||
 |
||||
| YELLOWSTONE
EXPLOSION COMPARISONS
10-6-03 - Yellowstone ground was 200 degrees 9-17-03 - People who have been at Yellowstone are saying that more
and more areas are being
9-12-03 - WHAT'S NEW? USGS SAYS 'NOTHING'!!! YEAH RIGHT!!!! 9-10-03 - 3.3
9-7-03 - Numerous micro-quakes occurring
There is a bulge over 100 feet high in the bottom of Yellowstone
Lake. The area under the northern end of the lake near
ACTIVE VOLCANO LINKS AROUND THE WORLD YELLOWSTONE - (44o26'00"S 110o40'00"W), 2,805 m, UNITED STATES (Wyoming) MEDICINE LAKE -
(41o35'00"S
121o44'00"W), 2,412 m, UNITED STATES (California)
|
||||
| http://www.fotomotivy.cz/menu/priroda/index.php
http://www.cartage.org.lb/en/themes/Sciences/Astronomy/TheGalaxies/themilkyway/NatureoftheGalaxy/February13/February13.htm |
||||
| FAIR USE NOTICE: This page contains copyrighted material the use of which has not been specifically authorized by the copyright owner. Pegasus Research Consortium distributes this material without profit to those who have expressed a prior interest in receiving the included information for research and educational purposes. We believe this constitutes a fair use of any such copyrighted material as provided for in 17 U.S.C § 107. If you wish to use copyrighted material from this site for purposes of your own that go beyond fair use, you must obtain permission from the copyright owner. | ||||
|
|