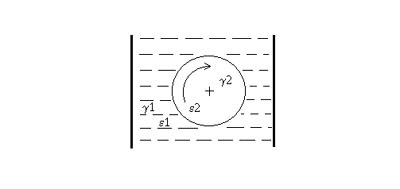

This rotation is produced by forces of field only and it is real free energy system that can take energy from inner structure of potential field. If we'll can to describe the mechanism of this effect we'll can increase the power of the system in industrial application level. So, why it is working?

By my opinion, there are some difference in conditions for polarization of the rotor and molecules of the liquid or gas those are surrounding the rotor since there is difference in permittivity and conductivity. By this reason the molecules are polarized both by field of electrodes and by field of rotor. The rotor is polarized in electric field of electrodes and molecules of liquid on its surface are polarized according to electric charge of the rotor, but not a field. So, the rotor is surrounded by "screen" of molecules on its surface. The electric charge of this screen partially compensate the field of electrodes.
When some angle is created by first initial rotation, there is some part of the rotor surface where molecules of liquid on surface of the rotor are in attraction to electrodes and it is the reason for rotation. After some angle the polarization is changed but new molecules are incoming in so called "sector of attraction" and the rotation always is accelerated.
This well-known effect of 1881 is very good example of possibility to produce the work in load by means of potential field only without any source of fuel.
